二叉树

94.二叉树的中序遍历

https://leetcode.cn/problems/binary-tree-inorder-traversal/description/?envType=study-plan-v2&envId=top-100-liked
给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

---

1. 递归

中序遍历就是先左->当前->右

import java.util.ArrayList;
import java.util.List;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    private List<Integer> TreeNodeList = new ArrayList<>();

    public List<Integer> inorderTraversal(TreeNode root) {
        return inorderHelper(root);
    }

    private List<Integer> inorderHelper(TreeNode root) {
        if (root == null){
            return TreeNodeList;
        }
        inorderHelper(root.left);
        TreeNodeList.add(root.val);
        inorderHelper(root.right);
        return TreeNodeList;
    }
}

时空复杂度都是O(n)

2. 迭代

递归隐式维护了一个栈，迭代就要显式维护一个栈

依次向左遍历，并把元素依次入栈，直到左孩子为空，开始依次出栈，直到栈空；

之后出栈一个，这个即为要处理的当前元素，把它加入结果后再开始对右子树准备处理右子树

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();//pop是出栈
            result.add(cur.val);
            cur = cur.right;
        }
        return result;
    }
}

时空依然都是O(n)

3. Morris 中序遍历

考虑使用二叉树本身的结构来替代栈，从而降低空间复杂度

上面的空间复杂度的核心是，当我们遍历完左侧，需要用栈（或者调用栈）来记录我们要回到哪个节点

可以考虑使用前驱节点来替代（中序遍历当前节点的上一个，也就是左子树的最右侧节点），让它指向当前节点即可

import java.util.ArrayList;
import java.util.List;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        while (root != null){
            if (root.left != null){
                TreeNode predecessor = root.left;
                while (predecessor.right != null && predecessor.right != root){
                    predecessor = predecessor.right;
                }
                if (predecessor.right == null){
                    predecessor.right = root;
                    root = root.left;
                }else {//左树已经访问完了
                    predecessor.right = null;
                    result.add(root.val);
                    root = root.right;
                }
            }else {
                result.add(root.val);
                root = root.right;
            }
        }
        return result;
    }
}

把这个再看看吧

104. 二叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/?envType=study-plan-v2&envId=top-100-liked
给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3
示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100

---

深度优先搜索。简单的想法就是深度优先，同时记录长度，每次遍历到叶节点更新一次长度。

一般的深度优先采取的是递归，很难记录到达叶节点的位置。

1. 深度优先搜索

如果使用递归深度优先，考虑分解。

最高高度 = max(左子树高度，右子树高度) + 1。

基本情况就是root == null返回0

时间复杂度：平均的话是T(n) = 2T((n-1)/2) + O(1) 。本地O（1），子问题n^(log2_2) 就是n，因此最终时间复杂度O(n)。也可以直接整体分析，每次对每个节点的调用本地操作都是O(1),但是要对每个节点调用一次。

空间复杂度：调用栈最多调用二叉树高度，最差是O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
    public int maxDepth(TreeNode root) {
        return maxDepthHelp(root);
    }
    private int maxDepthHelp(TreeNode root){
        if (root == null){
            return 0;
        }
        return Math.max(maxDepthHelp(root.left),maxDepthHelp(root.right)) + 1;
    }
}

2. 广度优先

List<Integer> levelOrder(TreeNode root) {
    //初始化一个队列,作为遍历过程中的临时储存。
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    //初始化一个列表储存结果
    List<Integer> result = new ArrayList<>();
    while (!queue.isEmpty())
    {
        TreeNode node = queue.poll();//出队
        result.add(node.val);
        if(node.left != null){
            queue.offer(node.left);
        }
        if(node.right != null)
        {
            queue.offer(node.right);
        }
    }
    return result;
}

也可以采用广度优先,上面是标准的广度优先遍历

广度优先搜索要先进先出，采用queue。每搜索一层，高度+1.关键在于怎么判断搜索完了一层。

可以在每次循环的开始，先获取当前queue中的元素个数，这个实际上就是本层的个数。然后采用for循环，直接把这层的元素全部出队并把对应的子节点放入，同时depth++即可。

 import java.util.LinkedList;
import java.util.Queue;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();//双向链表的队列实现
        int depth = 0;
        queue.add(root);
        while (!queue.isEmpty()){
            int thisLevelSize = queue.size();
            for (int i = 0; i < thisLevelSize; i++) {
                TreeNode node = queue.poll();
                if (node.left != null){
                    queue.add(node.left);
                }
                if (node.right != null){
                    queue.add(node.right);
                }
            }
            depth++;
        }
        return depth;
    }
}

时空都是O(n)

注意：

操作	LinkedList (双向链表)	ArrayDeque (循环数组)	解释
入队 (add/offer)	O(1)	Amortized O(1)	LinkedList 只是在尾部添加一个新节点并更新指针。ArrayDeque 在数组尾部添加元素，绝大多数情况是 O(1)，但如果数组满了，需要进行一次 O(n) 的扩容和复制操作。不过，由于扩容不是每次都发生，所以平摊下来（Amortized）的时间复杂度是 O(1)。
出队 (poll/remove)	O(1)	O(1)	LinkedList 只是移除头节点并更新指针。ArrayDeque 只是移动头指针的索引，并不会移动数组中的其他元素，所以也是 O(1)。
内存使用	更高	更低	这是 ArrayDeque 的巨大优势。LinkedList 的每个元素都需要一个额外的 Node 对象来包装，这个对象本身以及它内部的 prev 和 next 引用都会占用额外的内存。而 ArrayDeque 直接将对象存储在数组中，内存开销小得多。
CPU 缓存友好度	差	好	这是另一个关键性能优势。ArrayDeque 的元素在内存中是连续存储的，这使得 CPU 在访问一个元素后，可以很高效地预加载它旁边的元素到高速缓存（Cache）中，这被称为“缓存局部性”（Cache Locality）。而 LinkedList 的节点在内存中是分散的，访问下一个节点可能会导致“缓存未命中”（Cache Miss），需要从主内存中重新加载，速度慢得多。

实际上这里最好用ArrayDeque来作为实现更好。

226. 翻转二叉树

https://leetcode.cn/problems/invert-binary-tree/description/?envType=study-plan-v2&envId=top-100-liked

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例 1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]
示例 2：
输入：root = [2,1,3]
输出：[2,3,1]
示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

---

简单的想法就是分治递归：

翻转左子树，翻转右子树，再把左右子树调换（翻转本层）。

基本情况：如果是null，直接返回

时间复杂度：每个节点要调用一次，每次本地操作成本是O(1),因此总体是O(n)

空间复杂度：调用高度次，因此O(h),最差就是O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        TreeNode leftOld = invertTree(root.left);
        TreeNode rightOld = invertTree(root.right);
        root.left = rightOld;
        root.right = leftOld;
        return root;
    }
}

2. 使用栈来代替函数调用栈

上面实际上是深度优先搜索。可以使用一个栈来代替函数调用栈，把迭代转换成递归

具体来说，使用循环，每次只要栈不为空，就把节点出栈，把它的左右子节点交换，之后再把子节点入栈。

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Stack;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        Deque<TreeNode> stack = new ArrayDeque<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode cur = stack.pop();

            TreeNode temp = cur.left;
            cur.left = cur.right;
            cur.right = temp;

            if (cur.left != null) {
                stack.push(cur.left);
            }
            if (cur.right != null) {
                stack.push(cur.right);
            }
        }
        return root;
    }
}

注意： Java中使用ArrayDeque来实现栈最好，但是ArrayDeque没有实现接口stack，一般使用deque作为栈即可，不适用stack接口。

上面使用栈的解法相当于是前序遍历。

3. 广度优先搜索

也可以使用广度优先

创建一个队列

把root放入

队列中取出一个节点，cur非null则交换子节点

之后把cur子节点入队

import java.util.ArrayDeque;
import java.util.Queue;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);
        while (!queue.isEmpty()){
            TreeNode cur = queue.poll();
            if (cur != null){
                TreeNode temp = cur.left;
                cur.left = cur.right;
                cur.right = temp;
            }
            if (cur.left!=null){
                queue.add(cur.left);
            }
            if (cur.right != null){
                queue.add(cur.right);
            }
        }
        return root;
    }
}

101. 对称二叉树

https://leetcode.cn/problems/symmetric-tree/description/?envType=study-plan-v2&envId=top-100-liked

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

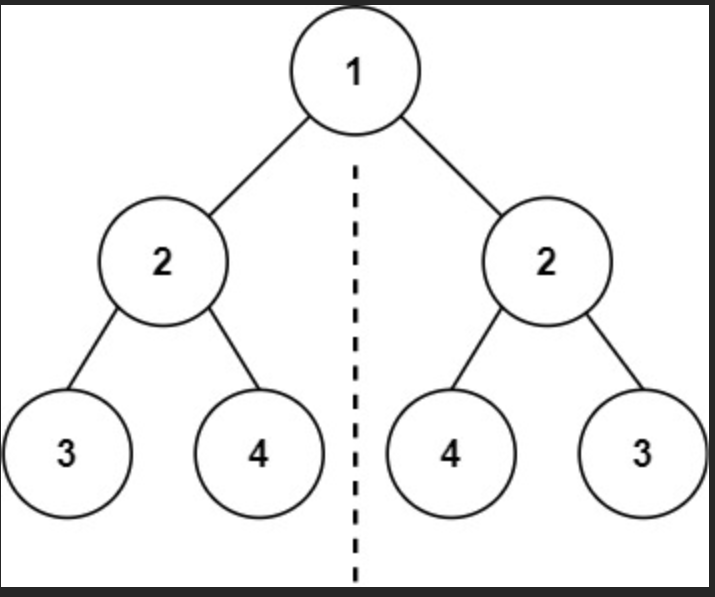
输入：root = [1,2,2,3,4,4,3]
输出：true
示例 2：

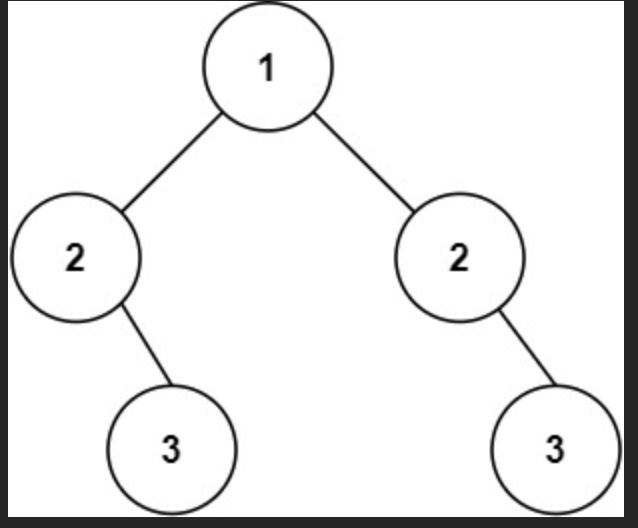
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

---

分治递归：

基本情况：为空或者只有一个节点天然对称

左右子树关于对称轴对称。

也就是要满足，

1. 根节点必须相等
2. left_tree的左子树要和right_tree的右子树对称
3. left_tree的右子树要和right_tree的左子树对称

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null){
            return true;
        }
        return help(root.left,root.right);
    }
    private boolean help(TreeNode node1,TreeNode node2){
        if ((node1 == null && node2!=null) ||(node1 != null && node2 == null)){
            return false;
        }
        if (node1 == null && node2 == null){
            return true;
        }
        if (node1.val == node2.val){
            return help(node1.left,node2.right) && help(node1.right,node2.left);
        }else {
            return false;
        }
    }
}

时间复杂度：O(n).递归树中最坏每个节点要调用一次，每个节点的本地调用都是O(1)

空间：O(n),递归到叶节点返回。最差情况退化成两个链表，深度O(n/2)

如下

      1
     / \
    2   2
   /     \
  3       3
 /         \
4           4

实际上上面的方法算是一种深度优先。先深入两条路径直到叶节点比较是否对称

2. 迭代，BFS

使用一个队列，一次镜像入队，比较节点值是否相同

 import java.util.LinkedList;
import java.util.Queue;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root.left);
        queue.offer(root.right);
        while (!queue.isEmpty()){
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();
            if (left == null && right == null){
                continue;
            }
            if (left == null || right == null){
                return false;
            }
            if (left.val != right.val){
                return false;
            }
            queue.offer(left.left);
            queue.offer(right.right);
            queue.offer(left.right);
            queue.offer(right.left);
        }
        return true;
    }
    
}

时间复杂度: O(n)。每个节点都要出队入队比较一次，非叶节点还要访问子节点，都是常数操作

空间复杂度：O(n).队列最大是叶节点，O(2^(logn)) = O(n)

543. 二叉树的直径

https://leetcode.cn/problems/diameter-of-binary-tree/description/?envType=study-plan-v2&envId=top-100-liked

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

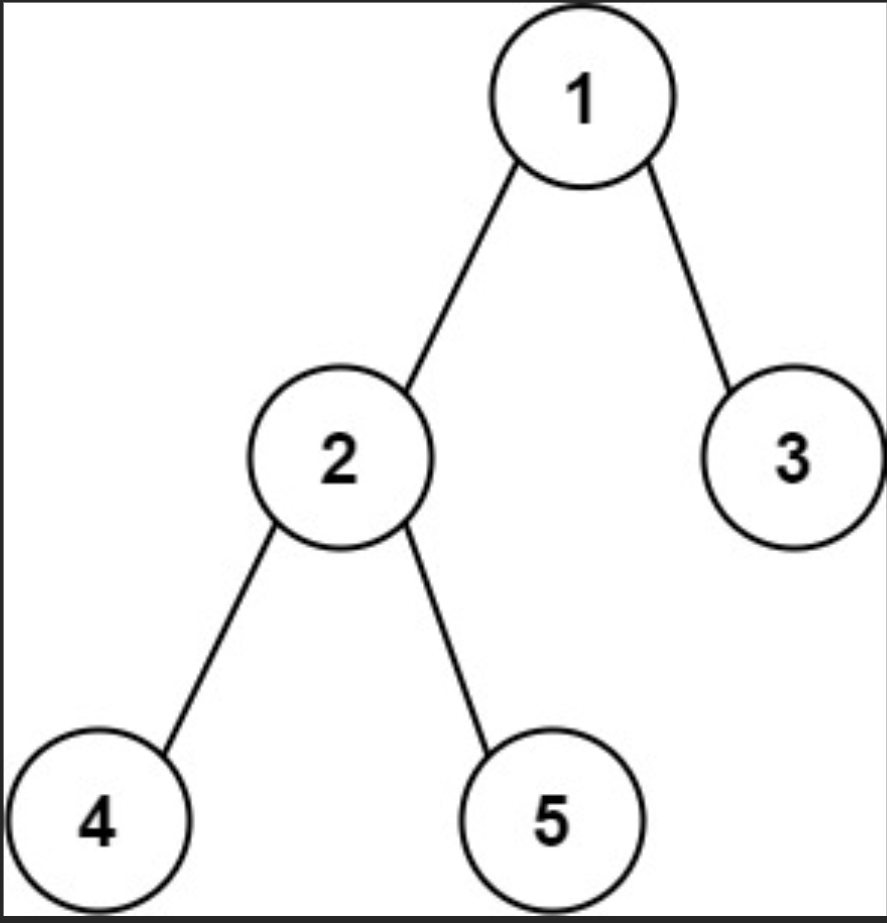
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2：

输入：root = [1,2]
输出：1

提示：

树中节点数目在范围 [1, 104] 内
-100 <= Node.val <= 100

---

对于每个节点，经过这个节点的最大路径都是他的左子树最大深度和右子树最大深度之和。

但是记得实现的时候要保存左右子树的深度以便让父节点使用避免重复计算，记忆化搜索。可以直接返回调用节点的深度即可，方便父节点直接算出对应子树深度

维护一个最大变量

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
    int maxLength = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxLength;
    }
    private int maxDepth(TreeNode node){
        if (node == null){
            return 0;
        }
       //算出左右子树的高度，并且期间副作用把maxLength更新为左右子树的最大直径的最大值。
       //事实上，这实际上也是个后续遍历

        int max_left = maxDepth(node.left);
        int max_right = maxDepth(node.right);
        //更新最大直径
        maxLength = Math.max(maxLength,max_left + max_right);
        
        
        
        //把本树的最大高度更新
        int depth = Math.max(max_left,max_right) + 1;
        return depth;
    }
}

时间复杂度：O(n).要访问每个节点，每个节点的本地操作都是更新maxLength，算出depth并且返回，都是O(1),

空间复杂度:O(n).最差成为链表O(n)

102. 二叉树的层序遍历

https://leetcode.cn/problems/binary-tree-level-order-traversal/description/?envType=study-plan-v2&envId=top-100-liked

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]
示例 2：

输入：root = [1]
输出：[[1]]
示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

import java.util.*;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<List<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> temp = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                temp.add(cur.val);
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null){
                    queue.offer(cur.right);
                }
            }
            result.add(temp);
        }
        return result;
    }
}

时间复杂度：O(n)。遍历所有节点，每个节点都执行入队出队判空添加获取队列大小等常数操作，最终就是O(n)

空间复杂度：O(n).队列储存最大的一层，最差很平衡的情况，是n/2

108. 将有序数组转换为二叉搜索树

https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/?envType=study-plan-v2&envId=top-100-liked

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。（平衡二叉树 是指该树所有节点的左右子树的高度相差不超过 1。）

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

---

相当于已经给出了中序遍历的结果

根据这个中序遍历结果来构建平衡二叉树

感觉天然是递归的问题

先找到中间的一个数作为根节点，之后以它为界限划分成两个数组构建两个左右子树即可。

基本情况就是数组长度为0.

返回值返回头节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
}

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedHelper(nums,0,nums.length - 1);
    }
    private TreeNode sortedHelper(int[] nums,int left,int right){
        if (left > right){
            return null;
        }
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        TreeNode leftChild = sortedHelper(nums,left,mid - 1);
        TreeNode rightChild = sortedHelper(nums,mid + 1,right);
        root.left = leftChild;
        root.right = rightChild;
        return root;
    }
}

时间复杂度：O(n).要访问所有的数字，对于每个数字，要创建新节点，计算mid，给节点左右指针赋值，都是O(1),最终是O(n)

空间：O(logn).不计算储存空间的话，函数调用栈需要调用到函数最大深度，平衡树深度近似认为logn

98. 验证二叉搜索树

https://leetcode.cn/problems/validate-binary-search-tree/description/?envType=study-plan-v2&envId=top-100-liked

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true
示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

---

二叉树本身就是递归的，还是先考虑递归

基本情况就是头节点左右孩子均为null就认为是true

只有一个孩子的话也单独列出来作为基本情况，因为此时不对称不是递归的了

先判断是否满足左孩子<根节点<右孩子

之后要找到左子树最右边的数，它要小于根节点；以及右子树最左边的数，他要大于根节点，否则返回false

之后判断左子树，右子树是否是搜索树，有一个不是直接返回false

都满足返回true

这个方法可以，但是效率很低。如果是个退化成接近链表的，对于每个节点都要遍历其左子树或者右子树到头，总体来说复杂度O(n^2)

1. 递归时限定范围

根节点传入负无穷到正无穷范围（头节点可以随便取）

左子树范围要求必须是原本下限到根节点（双开区间）；

右子树必须是根节点到原本上限；

具体步骤

null直接返回true

检查当前node.val是否在min_val,max_val

检查左子树，确保左子树范围都在min_val和node.val

检查右子树

都为真返回true

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValid(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }
    private boolean isValid(TreeNode node,long min_val,long max_val){
        if (node == null){
            return true;
        }
        if (node.val <= min_val || node.val >= max_val){
            return false;
        }
        //相信isValid能够检查出来左子树和右子树本身是否是合法的搜索树并且所有节点的值范围都在给定的范围内
        return isValid(node.left, min_val, node.val) && isValid(node.right, node.val, max_val);
    }
}

时间复杂度：O(n).每个节点都要调用一次，每个节点的调用都是判空、判断范围、获取值和左右指针都是O(1).

空间:最深O(H)，H最差是n

2. 直接中序遍历。搜索树的中序遍历必然是个升序的，只要遍历过程中发现矛盾即可返回false

一般来说，对于需要借助递归的遍历，如果需要一边递归一边处理其他操作，通常我们会选择维护一个额外的成员变量或者给函数添加额外的参数。

特性	模式一：通过参数传递	模式二：通过成员变量维护
信息流	自上而下 (Top-Down)	顺序/全局 (Sequential/Global)
状态作用域	局部于当前递归路径	全局共享
函数纯度	高（无副作用）	低（有副作用）
线程安全	相对安全	不安全
适用问题	依赖 路径信息 或 父节点约束	依赖 遍历顺序 或 全局聚合结果 （比如需要上一个遍历的节点的信息）
我们的例子	验证BST (限定范围法)	验证BST (中序遍历法)

这个题计算维护一个成员变量prev表示上一个节点，只有当前节点比上一个节点大才

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    long prev ;//认为最初遍历前的上一个元素是无穷小,使用Long的最小值，确保比任何int都小
    public boolean isValidBST(TreeNode root) {
        prev = Long.MIN_VALUE;
        return inOrderDFS(root);
    }
    
    private boolean inOrderDFS(TreeNode node){
        if (node == null){
            return true;
        }
        //先检查左子树是否是中序遍历升序
        if(!inOrderDFS(node.left)){
            return false;
        }
        //检查中序遍历的上一个值和node.val是否满足升序
        if (node.val <= prev){
            return false;
        }
        //更新prev为当前节点
        prev = node.val;
        //比较右子树是否中序遍历升序
        return inOrderDFS(node.right);
    }
}

时间复杂度:O(n),遍历所有节点，每个节点都要判空，比较和prev，更新prev都是O(1)操作

空间：O(h),最差退化到O(n)

也可以使用迭代的中序遍历：

迭代的中序遍历：

poll,remove出队

pop出栈

1. 手动创建一个栈stack，cur初始化为root
2. 进行循环，条件是cur不为null或者stack非空
3. 循环内，首先第一步，只要cur不为空，就把cur入栈，之后就把cur更新为cur.left
4. cur为空则开始将cur指向stack.pop()，并把cur加入结果，之后cur更新为cur.right

实际上，压栈就是代表要去先访问左子树，出栈表示左子树已经遍历完了，现在访问cur，每个节点都是实际上在此刻被访问的，下一个更新为右孩子表示处理右子树去

具体到这个题，不必使用结果列表记录，维护一个prev，在第四步出栈的时候，和prev比较即可。

import java.util.ArrayDeque;
import java.util.Deque;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        long prev = Long.MIN_VALUE;
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
            while (cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            if (cur.val <= prev){
                return false;
            }
            prev =(long)cur.val;
            cur = cur.right;
        }
        return true;
    }
}

时间复杂度：O(n),要遍历整个节点，每个节点操作出栈出栈，比较更新prev都是O(1)

空间:O(H)，栈最差要储存高度个节点，因此最差是H=n,O(n)

230. 二叉搜索树中第 K 小的元素

https://leetcode.cn/problems/kth-smallest-element-in-a-bst/description/?envType=study-plan-v2&envId=top-100-liked

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1
示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

---

最最简单的想法就是中序遍历的第k个元素

时间复杂度O(h + k)?先找到最左侧节点，之后找到第k个直接返回就行，最差O(n);

空间递归实现的话O(k)，最差O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
     int count = 0;
     int result;
    public int kthSmallest(TreeNode root, int k) {
        inOrderSearchK(root,k);
        return result;
    }
    private void inOrderSearchK(TreeNode node,int k){
        if (node == null){
            return ;
        }
        if (count >= k){
            return;//剪枝：如果初始时count就相等或者更大了，说明之前已经找到了结果直接返回
        }
        inOrderSearchK(node.left,k);//相信函数可以找到左子树第k个数字（如果第k个数存在在左子树里面的话），并且更新count
        if (count >= k){
            return;//剪枝：如果左子树已经找到了，直接返回即可
        }
        count++;//访问了本节点，count需要加一
        if (count == k){
            result = node.val;
            return;
        }
        inOrderSearchK(node.right,k);
    }
}

迭代实现,占位

import java.util.ArrayDeque;
import java.util.Deque;

/**
 Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
            while (cur!= null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            k--;
            if (k == 0){
                return cur.val;
            }
            cur = cur.right;
        }
        return -1;
    }
}

时间：O(n)

空间:O(h)

3. 进阶要求

可以给每个节点保存一个表示以此节点为根的节点数目

这样，对于每个节点，如果他的左子树等于k-1，当前节点就是答案；如果小于k-1，k更新成k - (left + 1),Node更新为node.right;如果大于，node更新为node.right并且继续

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        MyBst bst = new MyBst(root);
        return bst.kthSmallest(k);
    }
}

class MyBst {
    TreeNode root;
    Map<TreeNode, Integer> nodeNum;

    public MyBst(TreeNode root) {
        this.root = root;
        this.nodeNum = new HashMap<TreeNode, Integer>();
        countNodeNum(root);
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        TreeNode node = root;
        while (node != null) {
            int left = getNodeNum(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    // 统计以node为根结点的子树的结点数
    private int countNodeNum(TreeNode node) {
        if (node == null) {
            return 0;
        }
        nodeNum.put(node, 1 + countNodeNum(node.left) + countNodeNum(node.right));
        return nodeNum.get(node);
    }

    // 获取以node为根结点的子树的结点数
    private int getNodeNum(TreeNode node) {
        return nodeNum.getOrDefault(node, 0);
    }
}

时间复杂度：预处理的时间复杂度为 O(N)，其中 N 是树中结点的总数；我们需要遍历树中所有结点来统计以每个结点为根结点的子树的结点数。搜索的时间复杂度为 O(H)，其中 H 是树的高度；当树是平衡树时，时间复杂度取得最小值 O(logN)；当树是线性树时，时间复杂度取得最大值 O(N)。

空间复杂度：O(N)，用于存储以每个结点为根结点的子树的结点数。

4. AVL

199. 二叉树的右视图

https://leetcode.cn/problems/binary-tree-right-side-view/description/?envType=study-plan-v2&envId=top-100-liked

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

示例 2：

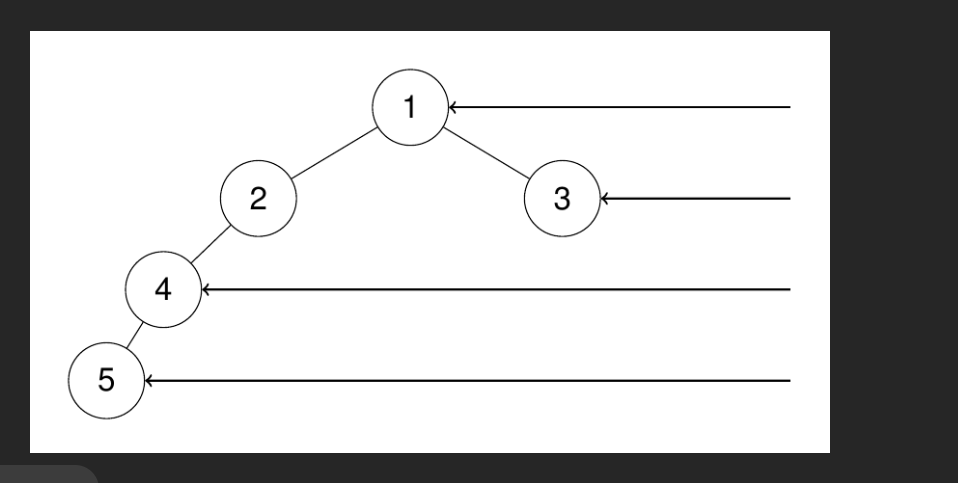
输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

输入：root = [1,null,3]

输出：[1,3]

示例 4：

输入：root = []

输出：[]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

---

右视图实际上就是最高的、并且最右侧的元素

可以先固定高度，找出每个高度上最右侧的元素，之后高度逐渐增加即可

这样是典型的层序遍历。

import java.util.*;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> queue = new ArrayDeque<>();
        result.add(root.val);
        queue.add(root);
        
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                if (cur.left != null){
                    queue.add(cur.left);
                }
                if (cur.right != null){
                    queue.add(cur.right);
                }
            }
            if (!queue.isEmpty()){
            result.add(queue.peekLast().val);
            }
            
        }
        return result;
    }
}

时间复杂度:O(n)

空间复杂度：O(宽度) = O(n)

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }

        Queue<TreeNode> queue = new LinkedList<>(); // 使用 Queue 接口，更通用
        queue.offer(root); // offer 是更推荐的入队方法

        while (!queue.isEmpty()) {
            int levelSize = queue.size(); // 固定当前层的节点数量
            for (int i = 0; i < levelSize; i++) {
                TreeNode cur = queue.poll();

                // 如果是当前层的最后一个节点，就加入结果集
                if (i == levelSize - 1) {
                    result.add(cur.val);
                }

                // 先加左孩子，再加右孩子
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
        }
        return result;
    }
}

这个实现更常见

2. 深度优先

也可以深度优先

深度顺序为特殊的“根节点 -> 右节点 -> 左节点”

同时要记录遍历的深度

如果第一次访问到某个深度就加入结果，可以通过看result长度和深度是否相等判断

关于递归记录额外信息的变量：

1. 希望一个变量在递归“回溯”时能自动恢复到上一层的状态，就把它放进参数里。
2. 如果一个变量是所有递归调用共同协作要完成的最终目标，或者是一个需要被所有调用参考的共享信息板，就把它作为成员变量。

import java.util.ArrayList;
import java.util.List;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        result = new ArrayList<>();
        return DFS(root,0);
    }

    List<Integer> result;

    private List<Integer> DFS(TreeNode cur,int depth) {//depth是当前的深度，根节点深度认为是0
        if (cur == null) {
            return result;
        }
        if (depth == result.size()) {
            result.add(cur.val);
        }
        //访问右左侧，并且第一次到达高度后记录进result
        DFS(cur.right,depth+1);
        DFS(cur.left,depth+1);
        return result;
    }
}

时间:O(n)

空间:O(h)

114. 二叉树展开为链表

https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/description/?envType=study-plan-v2&envId=top-100-liked
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

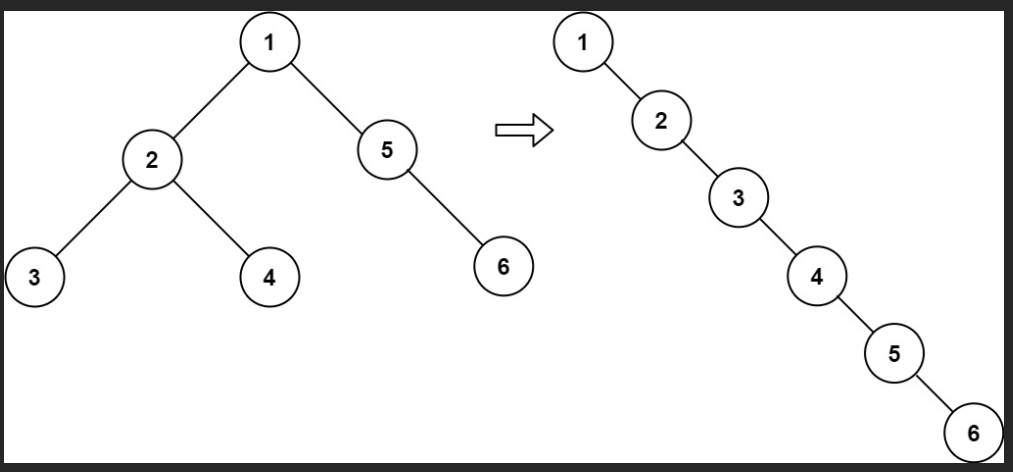
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

---

就直接前序遍历依次添加即可吧

但是题目给的solution方法是void

因此必须使用原来的节点不能创建新的节点

每个节点的left指针和right指针直接修改会导致无法访问左右子树

考虑使用变量记录指针

但是到了叶节点，左右指针均为null，无法修改right指针。因此考虑维护一个prev节点记录前序遍历的上一个节点

总之是，如果要直接修改cur.right，需要预知下一个前序遍历的节点，但这很难做到，因此不妨在遍历到cur时，让prev指向cur，这样就不需要预知了

时间O(n),空间O(n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
   }
}

class Solution {
    public void flatten(TreeNode root) {
        prev = new TreeNode();
        preOrder(root);
    }
    TreeNode prev;
    private void preOrder(TreeNode cur){
        if (cur == null){
            return;
        }
        prev.right = cur;
        TreeNode left = cur.left;
        TreeNode right = cur.right;
        cur.left = null;
        prev = cur;
        preOrder(left);
        preOrder(right);
    }
}

也可以迭代

class Solution {
    public void flatten(TreeNode root) {
        if (root == null) {
            return;
        }
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        TreeNode prev = null;
        while (!stack.isEmpty()) {
            TreeNode curr = stack.pop();
            if (prev != null) {
                prev.left = null;
                prev.right = curr;
            }
            TreeNode left = curr.left, right = curr.right;
            if (right != null) {
                stack.push(right);
            }
            if (left != null) {
                stack.push(left);
            }
            prev = curr;
        }
    }
}

2. 进阶：Morris算法

要实现进阶要求，常规的遍历算法不行。需要用Morris算法

• 标准递归/迭代遍历为何需要栈？

栈的核心作用是记忆。当程序从父节点 P 移动到其左子节点 L 时，必须记住 P，以便在处理完整个左子树后，能够返回到 P，然后再去处理 P 的右子树。这个“返回”的路径信息就存储在调用栈（递归）或我们手动维护的栈（迭代）中。

• Morris 遍历如何替代栈？
  Morris 遍历用一种极其巧妙的方式，将这个“返回路径”信息直接编码到了树的结构中。它通过建立一个临时的“线索”或“桥梁”（predecessor.right = curr），实现了这个记忆功能：

记忆：这个线索从左子树的最右节点（即中序遍历下 curr 的前驱）指向 curr 本身。

返回：当左子树的遍历走到了这个最右节点时，它会通过这个线索指针，直接跳转回 curr 节点，就像递归调用返回一样。

恢复：在“返回”之后，算法会断开这个临时线索，将树的结构恢复原状。

 public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
   }
}

class Solution {
    public void flatten(TreeNode root) {
        TreeNode cur = root;
        while (cur != null){
            if (cur.left != null){
                TreeNode predecessor = cur.left;
                while (predecessor.right != null){
                    predecessor = predecessor.right;
                }
                predecessor.right = cur.right;
                cur.right = cur.left;//右指针指向下一个
                cur.left = null;

            }
            cur = cur.right;//访问前序遍历下一个元素，也就是现在的右孩子
        }
    }

}

时间：

内层循环 while (predecessor.right != null) 会让 predecessor 指针移动。

让我们换个角度，不看单次循环，而是看整个算法生命周期中，predecessor 指针总共移动了多少步？

predecessor 指针只会在节点的左子树中，沿着右侧链向下移动。

结论是：树中的每一条右子边，最多只会被 predecessor 指针遍历一次。

为什么？假设 predecessor 正在为 curr 节点服务，它遍历了 A -> B 这条右子边。之后，curr 会移动到 A 所在的左子树内部。未来的任何 predecessor 搜索都只会在更深层的、尚未被处理的子树中进行，它再也没有机会回到 A -> B 这条边上进行搜索了。

树中总共有 n-1 条边。predecessor 指针只会沿着右子边移动。所以 predecessor 指针移动的总步数（即内层循环中 predecessor = predecessor.right 的总执行次数）严格小于边的总数 n-1。

所以，所有内层循环加起来的总工作量是 O(n)。

105. 从前序与中序遍历序列构造二叉树

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/?envType=study-plan-v2&envId=top-100-liked

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

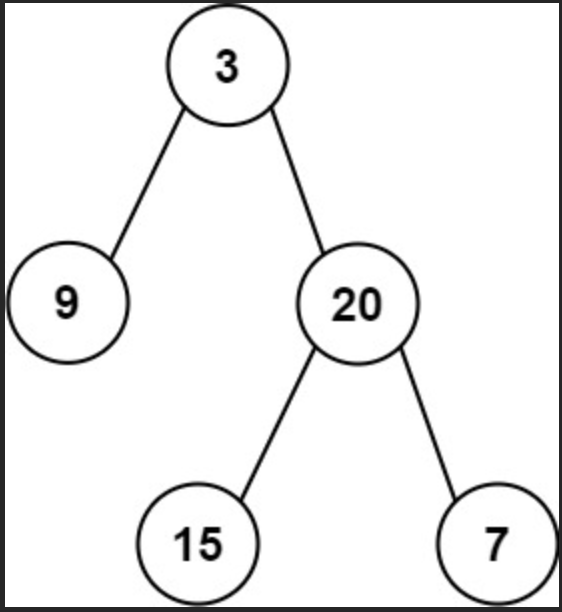
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

---

可以考虑分治

前序遍历的首元素必定是根节点，在中序遍历数组中找到根节点，索引记为mid，根节点左侧都是左子树部分,leftTreeSize = mid - inLeft，根节点右侧都是右子树部分；对于前序遍历，从索引为preLeft + 1开始长度为leftTreeSize的区间是左子树的前序遍历，也就是[preLeft+1,preLeft + leftTreeSize];[preLeft+leftTreeSize+1,末尾]是右子树的前序遍历

划分成了更小的子问题，根据左右子树的前序中序遍历构建两个子树，之后接到根节点两侧即可

基本情况：当中序前序长度为0，返回null

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 public class TreeNode {
    int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
 }

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeReverse(preorder,inorder,0, preorder.length-1,0,inorder.length-1);
    }
    private TreeNode buildTreeReverse(int[] preorder,int[] inorder,int preLeft,int preRight,int inLeft,int inRight){
        if (preLeft > preRight){
            return null;
        }
        int rootVal = preorder[preLeft];
        TreeNode root = new TreeNode(rootVal);
        int mid = 0;
        for (int i = inLeft; i <= inRight; i++) {
            if (inorder[i] == rootVal){
                mid = i;
                break;
            }
        }
        int leftTreeSize = mid - inLeft;
        TreeNode leftNode = buildTreeReverse(preorder,inorder,preLeft + 1,preLeft + leftTreeSize,inLeft,mid-1);//边界的处理务必注意，不得硬编码：比如使用0，1或者preorder.length()等，要使用传入的参数 preLeft，preRight等
        TreeNode rightNode = buildTreeReverse(preorder,inorder,preLeft+leftTreeSize+1,preRight,mid+1,inRight);
        root.left = leftNode;
        root.right = rightNode;
        return root;
    }
}

查找mid非常耗时，可以用哈希表记录inorder中每个数对应的索引把复杂度从O(n^2)（如果树退化成链表，每个for循环都是O(k),调用n次，O(1+……+n)）优化到O(n)

import java.util.HashMap;
import java.util.Map;

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i],i);
        }
        return buildTreeReverse(preorder, inorder,map, 0, preorder.length - 1, 0, inorder.length - 1);
    }

    private TreeNode buildTreeReverse(int[] preorder, int[] inorder,Map<Integer,Integer>map, int preLeft, int preRight, int inLeft, int inRight) {
        if (preLeft > preRight) {
            return null;
        }
        int rootVal = preorder[preLeft];
        TreeNode root = new TreeNode(rootVal);
        int mid = map.get(rootVal);
        int leftTreeSize = mid - inLeft;
        TreeNode leftNode = buildTreeReverse(preorder, inorder, map,preLeft + 1, preLeft + leftTreeSize, inLeft, mid - 1);//边界的处理务必注意，不得硬编码：比如使用0，1或者preorder.length()等，要使用传入的参数 preLeft，preRight等
        TreeNode rightNode = buildTreeReverse(preorder, inorder, map,preLeft + leftTreeSize + 1, preRight, mid + 1, inRight);
        root.left = leftNode;
        root.right = rightNode;
        return root;
    }
}

时间:O(n)

空间：O(n)

437. 路径总和 III

https://leetcode.cn/problems/path-sum-iii/?envType=study-plan-v2&envId=top-100-liked

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

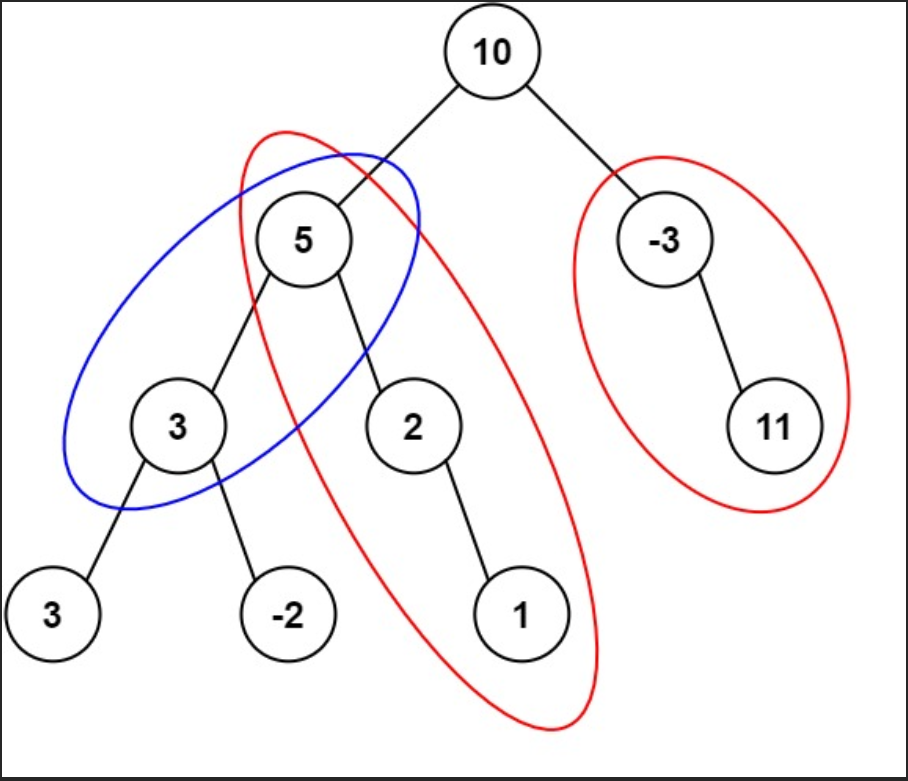
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

---

感觉是回溯算法

但是题目要求路径可以从任意节点开始

需要调用另一个函数进行遍历所有节点，计算以这个节点为起点的所有符合要求的路径

import java.util.ArrayList;
import java.util.List;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}


class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if (root == null){
            return 0;
        }
        int count = sumFrom(root,targetSum);
        count += pathSum(root.left,targetSum);//计算左子树路径和
        count += pathSum(root.right,targetSum);
        return count;
    }


    private int sumFrom(TreeNode root, long sum) {
        if (root == null){
            return 0;
        }
        long remaining = sum - root.val;
        int result = 0;
        if (remaining == 0){
            result++;
        }
        result += sumFrom(root.left,remaining);//相信sumFrom可以计算以左孩子为起点的所有等于remaining的路径的数目
        result += sumFrom(root.right,remaining);//可以看作隐式回溯，函数调用栈把上一个调用的remaining销毁了，回退到了本层remaining
        return result;
    }
}

时间:O(n^2),最坏情况下链状二叉树，每个节点都要遍历之后所有的节点，时间复杂度是O(N^2)

空间：O(n)

2. 前缀和法

   1. 使用一个哈希表 prefixSumCount 来存储前缀和及其出现的次数。key 是前缀和，value 是该和出现的次数。
   2. 我们从根节点开始深度优先遍历，并维护一个从根到当前节点的路径和 currentSum。
   3. 在访问一个新节点时，我们将 currentSum 加上该节点的值。
   4. 此时，我们检查哈希表中是否存在 currentSum - targetSum 这个键。如果存在，说明从根到当前节点的路径上，存在一个前缀和，使得从那个前缀和对应的节点到当前节点的路径和恰好为 targetSum。我们将 prefixSumCount.get(currentSum - targetSum) 的值累加到最终结果 result 中。
   5. 更新哈希表，将 currentSum 的计数加 1。
   6. 递归地访问当前节点的左、右子节点。
   7. 关键一步（回溯）： 在结束对当前节点及其子树的访问，即将返回上一层时，需要将 currentSum 在哈希表中的计数减 1。这是为了确保我们记录的前缀和只属于当前从根到父节点的路径，不会影响到兄弟节点的计算。

前缀和（从根节点到这个节点）。

那么从A到B的和就是B的前缀和减去A的父节点前缀和。

因此对于根节点要额外创建一个虚拟节点并认为前缀和为0

import java.util.HashMap;
import java.util.Map;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */


public class TreeNode {
   int val;
   TreeNode left;
   TreeNode right;

   TreeNode() {
   }

   TreeNode(int val) {
      this.val = val;
   }

   TreeNode(int val, TreeNode left, TreeNode right) {
      this.val = val;
      this.left = left;
      this.right = right;
   }
}

class Solution {
   public int pathSum(TreeNode root, int targetSum) {
      Map<Long, Integer> prefixSumCount = new HashMap<>();
      prefixSumCount.put(0L,1);
      return dfs(root,0,targetSum,prefixSumCount);
   }

   private int dfs(TreeNode node, long currentSum, int targetSum, Map<Long, Integer> prefixSumCount) {
      if (node == null) {
         return 0;
      }
      // 1. “选择”：将当前节点加入路径，更新 currentSum 和 prefixSumCount

      currentSum += node.val;
      int count = prefixSumCount.getOrDefault(currentSum - targetSum,0);
      prefixSumCount.put(currentSum, prefixSumCount.getOrDefault(currentSum, 0) + 1);
      
      //继续探索
      count += dfs(node.left, currentSum, targetSum, prefixSumCount);
      count += dfs(node.right, currentSum, targetSum, prefixSumCount);

      // 3. “撤销” (Unchoose/Backtrack)：
      // 将当前节点从路径中移除，恢复 prefixSumCount 的状态
      //保证当前节点的前缀只能被子树里面的节点看到，不被其他任何节点看到
      //当前节点以及他的子树都被探索完了，现在撤销影响把控制交还给父节点。

      prefixSumCount.put(currentSum, prefixSumCount.get(currentSum) - 1);
      
      //对于树的选择，因为只有两个选择，因此直接返回了
      return count;
   }
}

时间:O(n)

空间：O（n)

---

从广义上讲，这两种解法都运用了回溯的思想**。但它们在状态管理上的不同，导致了代码形式上的差异，一个看起来有“回退”步骤，另一个则没有。

回溯算法的核心思想

回溯算法的本质可以概括为 “选择、探索、撤销”：

1. 选择 (Choose)：在当前状态下，选择一个可行的选项向前走一步。
2. 探索 (Explore)：基于这个选择，递归地进入下一步，继续寻找解决方案。
3. 撤销 (Unchoose/Backtrack)：如果基于当前选择的探索最终没有找到解，或者已经探索完了所有可能性，那么就撤销刚才的选择，将状态恢复到选择之前的样子，然后尝试其他的选项。

这个“撤销”步骤是回溯算法的关键，它保证了在尝试完一个分支后，不会影响到对其他分支的探索。

---

解法一 (双重 DFS) 为何没有“显式”的回退步骤？

在这个解法中，回溯是隐式发生的，由递归函数的调用栈自动管理。

1. 状态是什么？ 这里的状态是 remaining (剩余的目标和)。
2. 状态是如何传递的？ remaining 是作为参数传递给下一次递归调用的。在 Java 中，基本类型 (long) 的参数是按值传递的。这意味着，当你调用 countPathsFrom(node.left, remaining) 时，是把 remaining 的一个副本传了进去。
3. 为什么不需要手动撤销？ 当 countPathsFrom(node.left, remaining) 这个函数执行结束并返回时，它对 remaining 副本的所有修改都随着函数栈的销毁而消失了。程序执行流回到 countPathsFrom(node, ...) 这个调用层级时，这里的 remaining 变量的值从未改变过。因此，它可以直接被用于对右子树的调用 countPathsFrom(node.right, remaining)。

简单来说，因为没有一个在所有递归调用中共享并被修改的数据结构，所以我们不需要手动去“撤销”修改。函数返回本身就起到了“撤销”和“恢复状态”的作用。

---

解法二 (前缀和) 为何需要“显式”的回退步骤？

在这个解法中，回溯必须是显式的。

1. 状态是什么？ 这里的状态不仅仅是 currentSum，更重要的是那个在所有递归调用中共享的哈希表 prefixSumCount。在 Java 中，对象（如 HashMap）是按引用传递的，所以在任何递归层级对 prefixSumCount 的修改都会影响到其他所有层级。
2. 为什么需要手动撤销？

• 当你处理完 node 的左子树 (dfs(node.left, ...) 返回) 后，你即将开始处理它的右子树 (dfs(node.right, ...)).
• 如果不执行撤销操作 (prefixSumCount.put(..., ... - 1))，那么在计算右子树的路径时，prefixSumCount 中仍然包含着当前节点 node 的前缀和。
• 这会产生错误，因为右子树中的路径不应该受到左子树路径的影响（路径只能向下）。node 的前缀和只应该对它的子节点可见。当探索完 node 的所有子树，准备返回到 node 的父节点时，必须将 node 造成的状态改变（即它自己的前缀和）从共享的 prefixSumCount 中移除。

总结

特性	解法一 (双重 DFS)	解法二 (前缀和)
回溯方式	隐式回溯	显式回溯
状态管理	通过函数调用栈和值传递的参数，状态是局部的。	通过引用传递的共享数据结构 (HashMap)，状态是全局的。
“撤销”操作	函数执行完毕返回，自动恢复上一层状态。	必须手动编码，在函数返回前恢复共享数据结构的状态。
本质	都是回溯思想的应用，即“深入探索，然后退回尝试其他可能”。	都是回溯思想的应用，即“深入探索，然后退回尝试其他可能”。

236. 二叉树的最近公共祖先

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/?envType=study-plan-v2&envId=top-100-liked

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

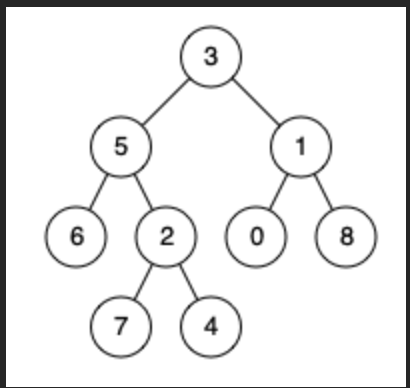
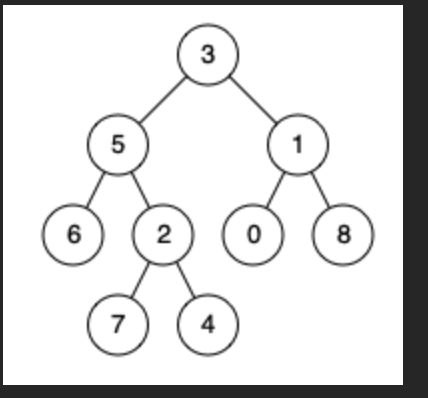
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 10^5] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

---

分治：

可以转化成求root左右子树中，是否存在最近公共祖先

基本情况就是子树根节点为null，或者根节点直接为p或q

考虑递归。

基本情况：null，或等于p，q，返回

递归：判断左子树，是否存在最近公共祖先。如果p，q都在左子树，会返回最近公共祖先；如果p,q只有一个在，会返回p或q；如果都不在返回null

判断右子树

根据情况返回

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode(int x) { val = x; }
 }

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q){
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if (left == null && right != null){
            return right;
        } else if (left != null && right == null) {
            return left;
        } else if (left != null && right != null) {
            return root;
        }else {
            return null;
        }
    }
}

时间O(n),空间O(h) = O(n)

下面的题解更好理解

一个节点node作为公共最近祖先的条件是，（左子树有pq中的一个&&右子树有pq中的一个）||((node==p)||(node==q)&&(左子树有pq||右子树有pq))

因此就转化成了判断左右子树有没有pq。

使用辅助函数dfs，并使用ans记录最近公共祖先

基本情况root为null返回false

搜索leftHas 和rightHas

判断是否找到最近公共祖先，如果找到直接更新

最后返回leftHas||rightHas

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

 public class TreeNode {
     int val;
     TreeNode left;
   TreeNode right;
     TreeNode(int x) { val = x; }
 }

class Solution {
     TreeNode result;
     private boolean dfs(TreeNode root,TreeNode p,TreeNode q){
         if (root == null){
             return false;
         }
         boolean leftHas = dfs(root.left,p,q);//相信dfs能找到左子树是否存在p或q，并且副作用可以把result更新为最近公共祖先（如果最近公共祖先存在在左子树）
         boolean rihgtHas = dfs(root.right,p,q);
         if ((leftHas&&rihgtHas) || (root==p || root==q)&&(leftHas||rihgtHas)){
             result = root;
         }
         return leftHas || rihgtHas || root == p || root == q;
         
     }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root,p,q);
        return result;
    }
}

124. 二叉树中的最大路径和

https://leetcode.cn/problems/binary-tree-maximum-path-sum/description/?envType=study-plan-v2&envId=top-100-liked

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

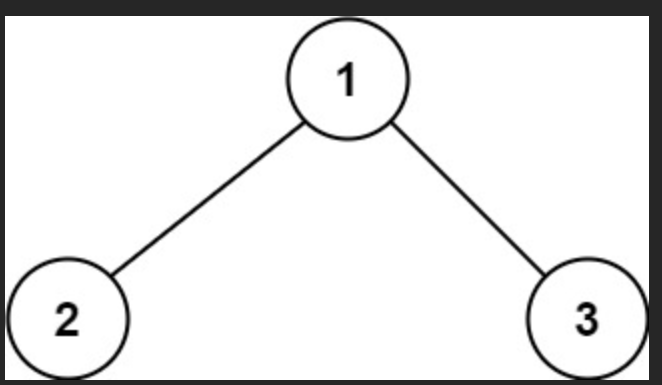
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：

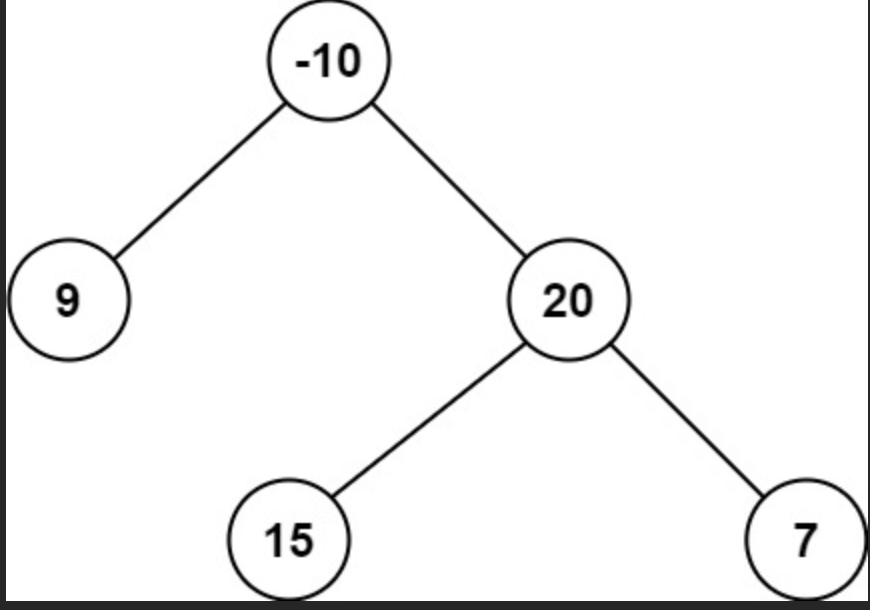
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

---

在 543. 二叉树的直径 问题中，发现经过某个节点的最大直径就是他的左右子树最大高度之和加1

对于这个问题，经过每个节点的最大路径和，都是它MAX（左子树最大和+node，右子树最大和+node，左子树最大和加上右子树最大和+node）

期间利用副作用维护一个maxSum

为了避免重复，递归函数返回以当前节点为起点的最大路径和

具体实现时注意：

1. 如果得到的子树最大和为负数，直接取0即可（代表着我们不用这条路径，贡献为0）
2. 基本情况，root为null，直接返回0
3. 初始化maxSum必须是Integer.MINVALUE，最初必须是个最小值，我们之后使用max才能保证不被初始值干扰
4. 递归函数返回的是以当前节点为起点的最大路径和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class TreeNode {
   int val;
   TreeNode left;
   TreeNode right;

   TreeNode() {
   }

   TreeNode(int val) {
      this.val = val;
   }

   TreeNode(int val, TreeNode left, TreeNode right) {
      this.val = val;
      this.left = left;
      this.right = right;
   }
}

class Solution {
   int maxSum = Integer.MIN_VALUE;

   private int maxPathSumHelper(TreeNode root) {
      if (root == null) {
         return 0;
      }
      int leftMaxSum = maxPathSumHelper(root.left);
      int rightMaxSum = maxPathSumHelper(root.right);
      int leftGain = Math.max(0,leftMaxSum);
      int rightGain = Math.max(0,rightMaxSum);
      maxSum = Math.max(leftGain+rightGain+root.val,maxSum);
      return Math.max(leftGain,rightGain) + root.val;
   }
   public int maxPathSum(TreeNode root){
      maxPathSumHelper(root);
      return maxSum;
   }
}

时间复杂度:O(n),空间O(H) = O(n)