20. 有效的括号

https://leetcode.cn/problems/valid-parentheses/description/?envType=study-plan-v2&envId=top-100-liked
给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = “()”

输出：true

示例 2：

输入：s = “()[]{}”

输出：true

示例 3：

输入：s = “(]”

输出：false

示例 4：

输入：s = “([])”

输出：true

示例 5：

输入：s = “([)]”

输出：false

提示：

1 <= s.length <= 104
s 仅由括号 ‘()[]{}’ 组成

必须数目是偶数
后来的左括号必须先和右括号匹配才行
用栈，遍历字符，遇到左括号就入栈，右括号就出栈，检查出栈的字符和右括号是否匹配直到末尾，如果栈空了就是匹配

import java.util.ArrayDeque;
import java.util.Deque;

class Solution {
    public boolean isValid(String s) {
        if (s.length() % 2 != 0) {
            return false;
        }
        Deque<Character> stack = new ArrayDeque<>();
        for (char c : s.toCharArray()) {
            if (c == '(' || c == '[' || c == '{')
            {
                stack.push(c);
            }else {
                if (stack.isEmpty()){
                    return false;
                }
                char b = stack.poll();
                if (c == ')' && b != '('){
                    return false;
                } else if (c == ']' && b != '[') {
                    return false;
                } else if (c == '}' && b != '{') {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

时间复杂度: O(n)

空间复杂度O(n)

下面是官方题解用哈希表简化代码

class Solution {
    public boolean isValid(String s) {
        int n = s.length();
        if (n % 2 == 1) {
            return false;
        }

        Map<Character, Character> pairs = new HashMap<Character, Character>() {{
            put(')', '(');
            put(']', '[');
            put('}', '{');
        }};
        Deque<Character> stack = new LinkedList<Character>();
        for (int i = 0; i < n; i++) {
            char ch = s.charAt(i);
            if (pairs.containsKey(ch)) {
                if (stack.isEmpty() || stack.peek() != pairs.get(ch)) {
                    return false;
                }
                stack.pop();
            } else {
                stack.push(ch);
            }
        }
        return stack.isEmpty();
    }
}

155.最小栈

https://leetcode.cn/problems/min-stack/?envType=study-plan-v2&envId=top-100-liked
设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
[“MinStack”,”push”,”push”,”push”,”getMin”,”pop”,”top”,”getMin”]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); –> 返回 -3.
minStack.pop();
minStack.top(); –> 返回 0.
minStack.getMin(); –> 返回 -2.

提示：

-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在非空栈上调用
push, pop, top, and getMin最多被调用 3 * 104 次

使用辅助栈

一个栈作为直接实现的栈dataStack

另一个作为辅助栈minStack，栈顶始终保持dataStack的最小值

具体实现：

push的元素要和minStack的栈顶比较，如果小就同时入minStack

pop出的元素要和minStack的栈顶比较，如果等于就同时minStack出栈

top就top

getMin就是minStack的top

import java.util.ArrayDeque;
import java.util.Deque;

class MinStack {

    Deque<Integer> dataStack;
    Deque<Integer> minStack;

    public MinStack() {
        this.dataStack = new ArrayDeque<>();
        this.minStack = new ArrayDeque<>();
    }

    public void push(int val) {
        dataStack.push(val);
        if (minStack.isEmpty()){
            minStack.push(val);
        }else {
            if (val <= minStack.peek()){
                minStack.push(val);
            }
        }
    }

    public void pop() {
        int curVal = dataStack.pop();
        if (curVal == minStack.peek()){//minStack.peek()返回的实际上是个Integer，这里比较的时候自动拆箱
            minStack.pop();
        }
    }

    public int top() {
        return dataStack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

时间复杂度:都是O(1)

空间复杂度:O(n)

394. 字符串解码

https://leetcode.cn/problems/decode-string/description/?envType=study-plan-v2&envId=top-100-liked
给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

测试用例保证输出的长度不会超过 105。

示例 1：

输入：s = “3[a]2[bc]”
输出：”aaabcbc”
示例 2：

输入：s = “3[a2[c]]”
输出：”accaccacc”
示例 3：

输入：s = “2[abc]3[cd]ef”
输出：”abcabccdcdcdef”
示例 4：

输入：s = “abc3[cd]xyz”
输出：”abccdcdcdxyz”

提示：

1 <= s.length <= 30
s 由小写英文字母、数字和方括号 ‘[]’ 组成
s 保证是一个有效的输入。
s 中所有整数的取值范围为 [1, 300]

第 1 步：识别问题的核心难点

先看简单的例子：

"3[a]" -> "aaa" (很简单，数字乘以字符)
"2[abc]3[cd]ef" -> "abcabc" + "cdcdcd" + "ef" (也很直接，就是顺序处理，做几次拼接)

再看复杂的例子：

"3[a2[c]]"

这里的核心难点是什么？是嵌套。我们不能简单地从左到右处理。在处理外层的 3[...] 时，我们必须先停下来，钻进去把内层的 2[c] 彻底解决掉，得到 "cc"，然后才能回头继续处理外层，把 "a" 和 "cc" 拼接成 "acc"，最后再重复 3 次。

关键洞察：处理一个问题（外层括号）依赖于另一个子问题（内层括号）的解决。并且，内层问题必须先于外层问题完成计算。

第 2 步：联想能够处理这种“后进先出”结构的工具

现在我们脑子里有一个关键词：“嵌套”或“后进先出”（Last-In, First-Out）。因为最后遇到的 [ (内层的)，需要最先处理完并和 ] 配对。

在计算机科学中，哪些数据结构或算法模式天生就是为了解决这种问题的？

递归 (Recursion)：一个函数调用自己来解决一个规模更小的、结构相同的问题。这和“处理一个括号，发现里面还有个括号，就先去处理那个小括号”的逻辑完全吻合。所以，递归是一个非常自然的想法。
栈 (Stack)：栈的本质就是 LIFO。它最经典的应用场景就是括号匹配和函数调用栈。
- 括号匹配：遇到左括号就入栈，遇到右括号就出栈检查。这和我们的问题很像！
- 函数调用：当你调用一个函数 A，A 又调用函数 B，计算机会把 A 的“执行现场”（比如局部变量、返回地址）压入一个调用栈，然后去执行 B。当 B 执行完毕返回时，再从栈里弹出 A 的“现场”来恢复执行。

思维跳跃：既然我们的问题和函数调用的嵌套结构如此相似，我们能不能手动模拟这个过程？用一个我们自己的栈，来“保存现场”和“恢复现场”。

第 3 步：设计“现场”需要保存什么信息

当我们准备钻进一个 [ 去处理子问题时，我们需要“暂停”当前的工作。那么，为了能在将来正确地“恢复”，我们需要保存哪些信息？

假设我们正在处理 ...prefix_string<K>[...]...，光标在 [ 处。

我们需要记住外层的重复次数 K。否则，当 [...] 内部解码完成后，我们不知道该把它重复多少遍。 -> 需要一个存数字的栈 countStack。
我们需要记住在遇到 K 之前，我们已经拼接好的字符串 prefix_string。否则，当 K[...] 解码完成后，我们不知道该把它拼接到谁的后面。 -> 需要一个存字符串的栈 stringStack。

到这里，用两个栈的方案就自然而然地浮现出来了。

第 4 步：确定操作规则

现在我们有了工具（两个栈）和目标（保存/恢复现场），就可以定义规则了：

遇到数字：这只是一个临时信息，先累加起来存到一个变量 multi 里。
遇到 [：这是“暂停”的信号。执行入栈操作，把 multi 和当前的 res 保存起来，然后清空它们，准备处理新一层。
遇到字母：这是当前层级的工作，直接拼接到当前的 res 后面。
遇到 ]：这是“恢复”的信号。子问题解决了。执行出栈操作，取出之前保存的重复次数和前缀字符串，然后按照 前缀 + 次数 * 当前结果 的公式组合起来，完成一次“返回”。

import java.util.ArrayDeque;
import java.util.Deque;

class Solution {
    public String decodeString(String s) {
        int multi = 0;
        StringBuilder res = new StringBuilder();
        Deque<Integer> countStack = new ArrayDeque<>();
        Deque<StringBuilder> stringStack = new ArrayDeque<>();
        for (char c : s.toCharArray()) {
            if (c >= '0' && c <= '9'){
                multi = multi * 10 + c - '0';
            }else if (c != '[' && c != ']'){
                res.append(c);
            }else if (c == '['){
                countStack.push(multi);
                multi = 0;
                stringStack.push(res);
                res = new StringBuilder();
            } else if (c == ']') {
                int repeatCount = countStack.poll();
                StringBuilder pre_res = stringStack.poll();
                for (int i = 0; i < repeatCount; i++) {
                    pre_res.append(res);
                }
                res = pre_res;
            }
        }
        return res.toString();
    }
}

时间复杂度：O(n)，n是解码后的总字符。每个s的字符遍历一次，除了’]’每个字符上的操作都是O(1),’]’的操作是O(K_i),设有m个’]’,最终是O(s-m) + O(mK_i)，k_i小于300，所以实际上是O(s+299m) = O(n),最终toString耗费O(n)，实际上最终就是O(n)

空间复杂度:O(s),最坏可能有接近s/2的元素入栈
2. 递归

依次向前遍历

遇到数字就更新multi

遇到字母就附加到res后面

遇到’[‘就递归调用

遇到’]’就返回

到结尾也返回。

契约：dfs能从给定的ptr开始，直到遇到对应的’]’，返回结果并且把ptr移到’]’的下一位

基本情况：到结尾或者遇到’]’

class Solution {
    public String decodeString(String s) {
        StringBuilder temp = dfs(s);
        return temp.toString();
    }
    int ptr = 0;
    private StringBuilder dfs(String s){
        int multi = 0;
        StringBuilder res = new StringBuilder();
        while (ptr < s.length()){
            char c = s.charAt(ptr);
            if (c >= '0' && c <= '9'){
                multi = multi * 10 + c - '0';
                ptr++;
            }else if (c == '['){
                ptr++;
                StringBuilder result = dfs(s);
                for (int i = 0; i < multi; i++) {
                    res.append(result);
                }
                multi = 0;
            }else if (c == ']'){
                ptr++;
                return res;
            }else {
                ptr++;
                res.append(c);
            }
        }
        return res;
    }
}

时间：和迭代一样

空间：O(s),最差开头一个’[‘,结尾一个’]’

739. 每日温度

https://leetcode.cn/problems/daily-temperatures/description/?envType=study-plan-v2&envId=top-100-liked

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:

输入: temperatures = [30,60,90]
输出: [1,1,0]

提示：

1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100

简单的想法就是每个元素向后遍历寻找高的，这个是O(N^2)

这样会有重复，对于每一天我们都“向后看”来寻找答案。

遍历到第i填时，能不能使用temp[i]这个信息去更新前面还在“等待升温”的日子的答案

举个例子，temperatures = [73, 74, 75, 71, 69, 72, 76, 73]

遍历到 73 (第0天)，后面是啥不知道，先放着。
遍历到 74 (第1天)，它比 73 高！所以第0天的答案就是 1 - 0 = 1。现在 74 自己在等待一个更高的温度。
遍历到 75 (第2天)，它比 74 高！所以第1天的答案是 2 - 1 = 1。现在 75 在等待。
遍历到 71 (第3天)，它比 75 低。那 75 只能继续等了。71 自己也在等待。
遍历到 69 (第4天)，它比 71 还低。现在 75, 71, 69 都在等待。
遍历到 72 (第5天)，它比 69 高！第4天的答案是 5 - 4 = 1。72 还比 71 高！第3天的答案是 5 - 3 = 2。但是 72 没有比 75 高，所以 75 还要继续等。现在 75 和 72 在等待。
…

显然，我们需要一个地方存放“还在等待更高温度”的地方，并且这些温度，从先等到后越来越低，在出去的时候符合后进先出。

可以使用单调栈。单调栈经常用来解决第一个小或者第一个大的问题

这里我们维护一个单调递减的栈，栈里面存放索引（为了计算日期）

具体思路：

初始化stack
初始化answer，默认0
遍历temperatures，每个索引i和对应的温度temp
1. 栈非空，并且temp大于栈顶，说明栈顶的日子等到了更高的温度。因此弹出索引记为prev_index,计算i-prev_index并且更新到结果，重复直到temp不大于栈顶或者栈为空
2. 处理完所有后，把当前索引压入栈内
answer就是结果，栈中依然有的元素没有等到因此对应的answer默认为0

import java.util.ArrayDeque;
import java.util.Deque;

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Deque<Integer> stack = new ArrayDeque<>();
        int[] answer = new int[temperatures.length];
        for (int i = 0; i < temperatures.length; i++) {
            int temp = temperatures[i];
            while (!stack.isEmpty() && temp > temperatures[stack.peek()]){
                int prev_index =  stack.poll();
                answer[prev_index] = i - prev_index;
            }
            stack.push(i);
        }
        return answer;
    }
}

时间复杂度:O(n),整体来说对于每个日期都要入栈一次，出栈一次，还有就是比较，比较成功总体合起来就是n次（因为最多n次出栈），比较失败也是n次，因此一共还是O(n)
空间:O(n),整体递减最差O(n)

84. 柱状图中最大的矩形

https://leetcode.cn/problems/largest-rectangle-in-histogram/description/?envType=study-plan-v2&envId=top-100-liked

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

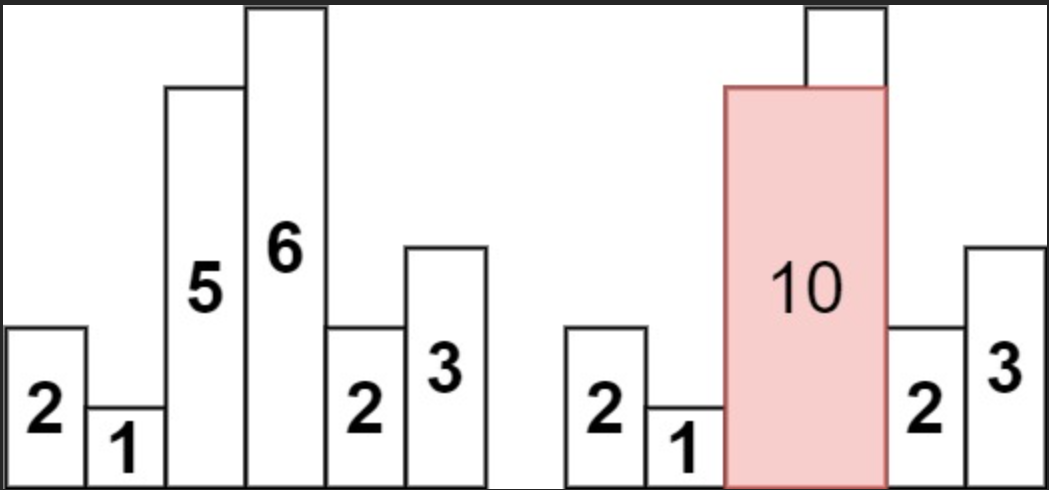
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10
示例 2：

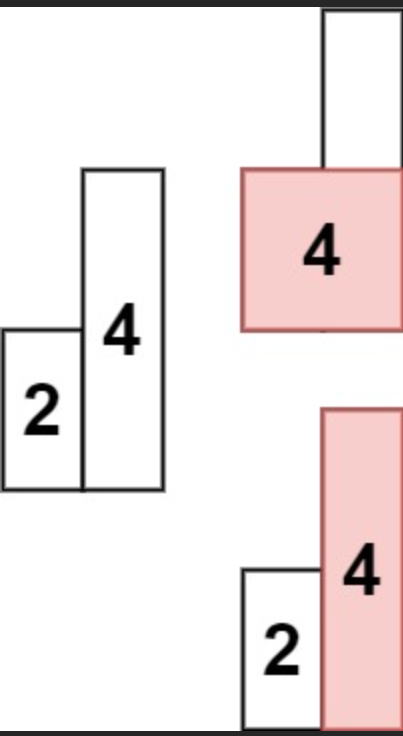
输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

首先是两个暴力解法，都超时：

按宽度枚举。两次遍历枚举所有边，中间维护minHeigh变量。时间复杂度O(n^2)
按高度枚举。遍历枚举所有高度，对于每个高度尽可能向左向右找到第一个比目标高度低的柱子作为左右边界。时间复杂度O(N^2)

关于2，可以优化。

因为我们还是要“第一个小的”，可以使用单调栈

我们维护一个单调递增栈

具体步骤

创建stack储存索引
遍历柱子。每个柱子，如果它比stack.peek()矮，就出栈，并且出栈的元素记为curHead，则当前遍历到的柱子是右侧第一个比curHead低的柱子也就是右边界，出栈后的栈顶左边界（关于这个，我们可以假设在新栈顶left_index和原栈顶mid_index之间存在k比curHead低，那么当遍历到k的时候，就会把left_index出栈，left_index就不该存在，矛盾））（就是以当前curHead为高度的最大宽度），维护更新maxArea。循环这个过程，直到栈空或者当前索引高度大于栈顶。之后把当前索引入栈
为了方便，我们在最左侧和最右侧都增加一个高度为0的柱子，确保所有柱子都会最终被出栈
其实相当于，在每个柱子出栈的时候，以该柱子为高，自动获得最大边界算出面积。

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

class Solution {
    public int largestRectangleArea(int[] heights) {
        Deque<Integer> stack = new ArrayDeque<>();
        int max_area = 0;
        List<Integer> new_heights = new ArrayList<>();
        new_heights.add(0);
        for (int i : heights) {
            new_heights.add(i);
        }
        new_heights.add(0);
        for (int i = 0; i < new_heights.size(); i++) {
            while (!stack.isEmpty() && new_heights.get(i) < new_heights.get(stack.peek())){
                int cur = stack.pop();
                int curHeigh = new_heights.get(cur);
                int length = i - stack.peek() - 1;
                max_area = Math.max(max_area,curHeigh * length);
            }
            stack.push(i);
        }
        return max_area;
    }
}

时间复杂度：整体来说，每个柱子都要入栈出栈一次，还要比较、计算，一共最多比较成功、计算n次，比较失败n次，最终是O(n)

空间复杂度：新列表O(n)，栈O(n)