200. 岛屿数量

https://leetcode.cn/problems/number-of-islands/?envType=study-plan-v2&envId=top-100-liked
给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
[‘1’,’1’,’1’,’1’,’0’],
[‘1’,’1’,’0’,’1’,’0’],
[‘1’,’1’,’0’,’0’,’0’],
[‘0’,’0’,’0’,’0’,’0’]
]
输出：1
示例 2：

输入：grid = [
[‘1’,’1’,’0’,’0’,’0’],
[‘1’,’1’,’0’,’0’,’0’],
[‘0’,’0’,’1’,’0’,’0’],
[‘0’,’0’,’0’,’1’,’1’]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

表格每个格子看作一个图的节点，记为(i,j),i，j分别是行列坐标

如果两个相邻的节点都是1，意味着这两个节点直接有一条边。

每当读取到一个新的未访问过的1，岛屿数目就加1，遍历和他相邻的所有节点，所有遍历到的节点都记为访问过（可以二维布尔数组，也可以直接原地改为-1）

整体上来说，每个节点都被访问一次。每次访问的各种操作都是O(1)

因此复杂度O(mn)

深度优先遍历

考虑深度优先遍历

class Solution {
    public int numIslands(char[][] grid) {
        int result = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1'){
                    result++;
                    dfs(i,j,grid);
                }
            }
        }
        return result;
    }
    private void dfs(int row, int col, char[][] grid){
        if (grid[row][col] == '2' || grid[row][col] == '0'){
            return;
        }
        grid[row][col] = '2';
        int[][] direction = new int[][]{{1,0},{0,1},{-1,0},{0,-1}};
        for (int[] dir : direction) {
            int newRow = row + dir[0];
            int newCol = col + dir[1];
            if (newRow >= 0 && newRow < grid.length && newCol >= 0 && newCol<grid[0].length){
                if (grid[newRow][newCol] == '1'){
                    dfs(newRow,newCol,grid);
                }
            }
        }
    }
}

代码逻辑可以优化如下，dfs把判断都放在开头,同时没必要引入’2’这个状态

class Solution {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }
        int result = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1') {
                    result++;
                    dfs(i, j, grid);
                }
            }
        }
        return result;
    }

    // 优化后的 DFS 方法
    private void dfs(int row, int col, char[][] grid) {
        // 1. 将所有终止条件（边界检查和格子状态检查）放在函数开头
        // 这样使得递归逻辑更清晰
        if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] != '1') {
            return;
        }

        // 2. 标记当前节点为已访问。可以直接改成'0'，也可以用'2'
        grid[row][col] = '0'; // 或者 '2'

        // 3. 向四个方向递归，循环体内不再需要任何if判断
        dfs(row + 1, col, grid);
        dfs(row - 1, col, grid);
        dfs(row, col + 1, grid);
        dfs(row, col - 1, grid);
    }
}

时间O(mn),空间O(mn)(最大岛屿面积mn)
2. 广度优先

import java.util.ArrayDeque;
import java.util.Queue;

class Solution {
    public int numIslands(char[][] grid) {
        int result = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1'){
                    result++;
                    bfs(grid,i,j);
                }
            }
        }
        return result;

    }

    private class node{
        char value = '2';
        int row = -1;
        int col = -1;
        public node(char value,int row,int col){
            this.value = value;
            this.col = col;
            this.row = row;
        }
    }
    private void bfs(char[][] grid, int row, int col) {
        Queue<node> queue = new ArrayDeque<>();
        queue.offer(new node(grid[row][col],row,col) );
        grid[row][col] = '0';
        int[][] direction = new int[][]{{1,0},{0,1},{-1,0},{0,-1}};
        while (!queue.isEmpty()){
            node node = queue.poll();
            int rowThisLoop = node.row;
            int colThisLoop = node.col;
            for (int[] dir : direction) {
                int newRow = rowThisLoop + dir[0];
                int newCol = colThisLoop + dir[1];
                if (newRow >= 0 && newRow < grid.length && newCol >= 0 && newCol<grid[0].length){
                    if (grid[newRow][newCol] == '1') {
                        queue.offer(new node(grid[newRow][newCol], newRow, newCol));
                        grid[newRow][newCol] = '0';
                    }
                }
            }
        }
    }
}

实际上上面可以不适用node类

import java.util.ArrayDeque;
import java.util.Queue;

class Solution {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }

        int result = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1') {
                    result++;
                    bfs(grid, i, j);
                }
            }
        }
        return result;
    }

    private void bfs(char[][] grid, int row, int col) {
        // 队列直接存储坐标数组 int[]{row, col}
        Queue<int[]> queue = new ArrayDeque<>();
        queue.offer(new int[]{row, col});
        grid[row][col] = '0'; // 标记为已访问

        int[][] direction = new int[][]{{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

        while (!queue.isEmpty()) {
            int[] current = queue.poll();
            int rowThisLoop = current[0];
            int colThisLoop = current[1];

            for (int[] dir : direction) {
                int newRow = rowThisLoop + dir[0];
                int newCol = colThisLoop + dir[1];

                if (newRow >= 0 && newRow < grid.length && newCol >= 0 && newCol < grid[0].length) {
                    if (grid[newRow][newCol] == '1') {
                        queue.offer(new int[]{newRow, newCol});
                        grid[newRow][newCol] = '0'; // 标记为已访问
                    }
                }
            }
        }
    }
}

时间O(mn),空间O(min(m,n)).画图可得，队列queue是在不断扩散的（一个斜着的正方形），最大是2sqrt(ming(m,n)),因此最终空间复杂度是O(min(m,n))

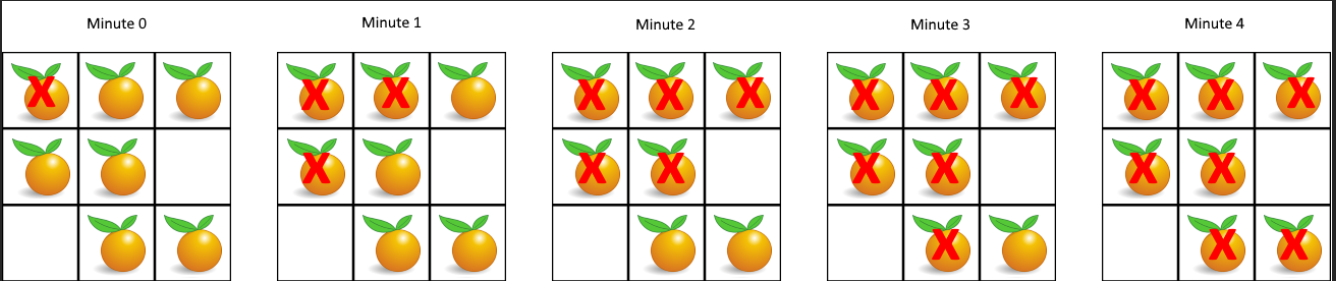
994. 腐烂的橘子

https://leetcode.cn/problems/rotting-oranges/description/?envType=study-plan-v2&envId=top-100-liked
在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，腐烂的橘子周围 4 个方向上相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4
示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行，第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。
示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2

把每个格子看成一个节点

先遍历，找出所有为2的节点

之后，对于每个为2的节点，只要相邻的是1都认为他们是邻节点，进行第一次腐化，minute加一

把新腐化的节点都放入一个列表。

之后再次腐化循环

直到所有1都被腐化或者没有和2相邻的1

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

class Solution {
    public int orangesRotting(int[][] grid) {
        
        Queue<int[]> rottedOrangesToProcess = new ArrayDeque<>();
        int loop = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 2) {
                    rottedOrangesToProcess.offer(new int[]{i, j});
                }
            }
        }
        while (!rottedOrangesToProcess.isEmpty()) {
            int size = rottedOrangesToProcess.size();
            for (int i = 0; i < size; i++) {
                int[] place = rottedOrangesToProcess.poll();
                List<int[]> rottedPlace = rot(grid, place[0], place[1]);
                for (int[] newPlace : rottedPlace) {
                    rottedOrangesToProcess.offer(newPlace);
                }
            }
            loop++;
        }
        boolean hasOne = false;
        boolean hasTwo = false;
        boolean hasZero = false;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 1) {
                    hasOne = true;
                }
                if (grid[i][j] == 2){
                    hasTwo = true;
                }
                if (grid[i][j] == 0){
                    hasZero = true;
                }
            }
        }
        if (hasOne){
            return -1;
        }
        if (hasZero && !hasTwo && !hasOne){
            return 0;
        }
        
        return loop - 1;

    }

    private List<int[]> rot(int[][] grid, int row, int col) {
        List<int[]> rottedPlace = new ArrayList<>();
        int[][] direction = new int[][]{{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
        for (int[] dir : direction) {
            int newRow = row + dir[0];
            int newCol = col + dir[1];
            if (newRow >= 0 && newRow < grid.length && newCol >= 0 && newCol < grid[0].length) {
                if (grid[newRow][newCol] == 1) {
                    grid[newRow][newCol] = 2;
                    rottedPlace.add(new int[]{newRow, newCol});
                }
            }
        }
        return rottedPlace;
    }
}

时间复杂度：O(n^2),遍历寻找2花费O(n^2),腐化过程最多访问O(n^2)个节点，每个节点的访问和其他操作都是O(1),最后检查结果也是O(n^2),最终O(n^2)

空间复杂度：主要是队列，这个队列最差O(m*n)。比如如下情况

2 1 2 1 2 1 ...
1 2 1 2 1 2 ...
2 1 2 1 2 1 ...
1 2 1 2 1 2 ...
...

只有在只有一个起点的时候，复杂度才是O(min(m,n)).

实际上上面的解法是个多源起点的BFS。

上面的代码可以优化。可以寻找2的时候记录1和0的个数。之后每次腐化一个节点1的个数就减少rottedPlace.size()。最终1，0的数据获取不必再次遍历。但是复杂度不变。

同时Loop的返回可以优化

import java.util.ArrayDeque;
import java.util.Queue;

class Solution {
    public int orangesRotting(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        Queue<int[]> queue = new ArrayDeque<>();
        int freshCount = 0;

        // 步骤 1: 第一次遍历，统计新鲜橘子并将腐烂橘子入队
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    freshCount++;
                } else if (grid[i][j] == 2) {
                    queue.offer(new int[]{i, j});
                }
            }
        }

        // 步骤 2: 处理边界情况
        if (freshCount == 0) {
            return 0;
        }

        int minutes = 0;
        int[][] directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

        // 步骤 3: BFS 过程
        while (!queue.isEmpty()) {
            // 增加 minutes 的时机很关键。
            // 上面本来的解法会导致即使最后一轮没有腐烂任何橘子，时间也会+1。
            // 所以更好的方式是，引入判断rottedInThisMinute，只有本轮有橘子腐烂才minute+1
            // 如果队列处理完后 freshCount > 0，则说明无法完成。
            
            int size = queue.size();
            boolean rottedInThisMinute = false;
            for (int i = 0; i < size; i++) {
                int[] current = queue.poll();
                for (int[] dir : directions) {
                    int newRow = current[0] + dir[0];
                    int newCol = current[1] + dir[1];

                    if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && grid[newRow][newCol] == 1) {
                        grid[newRow][newCol] = 2;
                        freshCount--;
                        queue.offer(new int[]{newRow, newCol});
                        rottedInThisMinute = true;
                    }
                }
            }
            
            // 如果在这一分钟内有新的橘子被腐烂，时间才加一
            if (rottedInThisMinute) {
                minutes++;
            }
        }

        // 步骤 4: 返回最终结果
        return freshCount <= 0 ? minutes : -1;
    }
}

207. 课程表

https://leetcode.cn/problems/course-schedule/description/?envType=study-plan-v2&envId=top-100-liked
你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对互不相同

每个课看成一个图得节点

需要整个图不能存在一个环

prerequisites就是边

这个图还是个有向图。

prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi

因此bi必然在ai前面

因此bi -> ai

似乎可以使用邻接矩阵先创造一个图，之后判断是否有环？还是邻接表？

事实上邻接表和邻接矩阵都能表示有向图和无向图

邻接表：每个节点对应的表对应的就是该节点指向的所有节点。如果无向则[i,j][j,i]都添加

邻接矩阵：[i,j]的值表示i指向j有边

邻接表空间复杂度：O(V + E)(O(V+E1+……En) = (V+E)),

邻接矩阵：O(V^2)

E对于无向图最多是C(V,2) = (v)(v-2)/2,有向图A(V,2) = V(V-1).

深度优先：

先创建邻接表，之后深度优先搜索判断是否有环

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<List<Integer>> adjacency = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            adjacency.add(new ArrayList<>());
        }
        for (int[] edge : prerequisites) {
            adjacency.get(edge[1]).add(edge[0]);//从edge[1]指向edge[0]
        }
        int[] visited = new int[numCourses];//visted[i]为1代表正在访问i，为2代表已经访问过该节点，并且确定了以该节点为起点的所有路径上都不存在环。visited为0表示还没访问过

        for (int i = 0; i < numCourses; i++) {
            // 只对尚未被访问过的节点进行DFS
            if (visited[i] == 0) {
                if (hasCycle(i, adjacency, visited)) {
                    return false;
                }
            }
        }
        return true;
    }
    
    //是个回溯算法
    private boolean hasCycle(int course, List<List<Integer>> adjacency, int[] visited) {//不能使用布尔的visited来表示是否被访问过。因为无法确定是某一条深度优先的路径重复访问造成的环，还是不同路径访问的。
        // 如果状态为 1，说明在本次DFS中再次访问到该节点，检测到环
        if (visited[course] == 1) {
            return true;
        }
        // 如果状态为 2，说明这个节点已经被其他路径安全访问过，无需重复检查（剪枝）
        if (visited[course] == 2) {
            return false;
        }

        // 将当前节点标记为“正在访问”
        visited[course] = 1;

        // 递归访问所有后续课程（做出选择）
        for (int nextCourse : adjacency.get(course)) {
            if (hasCycle(nextCourse, adjacency, visited)) {
                return true;
            }
        }

        // 将其标记为“已访问”。撤销选择（从当前路径移出，并且标记为2方便剪枝）
        visited[course] = 2;
        return false;
    }
}

时间复杂度：
O(V+E)。对于每个节点和每个边都会访问一次，每次访问都进行了O(1)操作（访问相邻，标记等）
空间复杂度：
O(V+E)

广度优先搜索

先回顾度的概念：度就是相邻节点个数。入度就是有向图中指向该节点的个数，出度反之

构造入度数组，入度为0的意味着没有先修课，可以学习，直接加入一个队列

只要队列不为空，学过的课程数目count++，并且把这个课程的所有后续课程的入度减一，如果有某个课程入度成为0把它入队

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] inDegree = new int[numCourses];
        List<List<Integer>> ad = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            ad.add(new ArrayList<>());
        }
        for (int[] edge : prerequisites){
            ad.get(edge[1]).add(edge[0]);
            inDegree[edge[0]]++;

        }
        
        Queue<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }
        int count = 0;
        while (!queue.isEmpty()) {
            int course = queue.poll();//这里不需要先得到int size = queue.size()，我们没有必要按层遍历
            count++;
            for (int nextCourse : ad.get(course)) {
                inDegree[nextCourse]--;
                if (inDegree[nextCourse] == 0){
                    queue.offer(nextCourse);
                }
            }
                
            
        }
        return count == numCourses;
    }
}

时间复杂度：每个顶点和边都要访问一次，每个边和顶点都是O(1)操作，因此时间复杂度O((V+E))

空间：邻接表O(V+E),队列O（V），因此O(V+E)

208. 实现 Trie (前缀树)

https://leetcode.cn/problems/implement-trie-prefix-tree/description/?envType=study-plan-v2&envId=top-100-liked
Trie（发音类似 “try”）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True

提示：

1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数总计不超过 3 * 104 次

出现在图这个章节，应该要用图

使用哈希表可以方便的查询插入

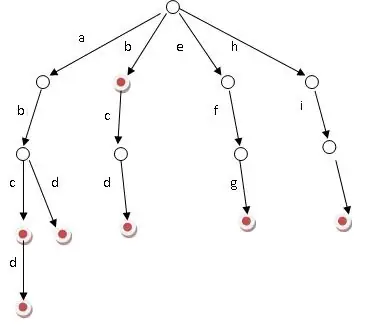
这个树实际上如下这个样子：

上面实际上就是一个有向无环图

每个节点都是一个字母，并且有一个结束标志。

从根节点开始到每个结束表示，路径组成的对应的单词

具体实现可以使用邻接表

通常的邻接表包含两个部分：所有节点的集合+每个节点的邻接点集合

但这里不需要。

这个特殊的图，我们保证从root能访问到所有其他节点，同时我们总是从root开始操作，因此只需要给每个节点构造一个邻接点的集合即可

具体的节点实现：

因为我们要可能频繁增删查改，所以邻接点的集合使用哈希表
一个布尔遍历表示是否是结束标志

注意这里根节点root实际上代表的是空字符

import java.util.HashMap;
import java.util.Map;

class Trie {
    private class TrieNode {
        Map<Character,TrieNode> map;
        boolean isAWOrdEnd = false;
        
        public TrieNode(){
            this.map = new HashMap<>();
        }
    }

    private TrieNode root;
    
    public Trie() {
        this.root = new TrieNode();
    }

    public void insert(String word) {
        int cur = 0;
        TrieNode curNode = root;
        while (cur < word.length()){
            char curChar = word.charAt(cur);
            if (!curNode.map.containsKey(curChar)){
                curNode.map.put(curChar,new TrieNode());  //整体可以替换为currentNode = currentNode.children.computeIfAbsent(ch, k -> new TrieNode());，调用computeIfAbsent 方法，这里ch会作为lambda表达式的参数传入

            }
            cur++;
            curNode = curNode.map.get(curChar);

        }
        curNode.isAWOrdEnd = true;
    }

    public boolean search(String word) {
        int cur = 0;
        TrieNode curNode = root;
        while (cur < word.length()){
            if (!curNode.map.containsKey(word.charAt(cur))){
                return false;
            }else  {
                curNode = curNode.map.get(word.charAt(cur));
                cur++;

            }
        }
        return curNode.isAWOrdEnd;
        //可以构建这个循环不变量来理解这个边界：在每次 for 循环（或 while 循环）的条件判断之前，curNode 变量总是指向代表前缀 word.substring(0, i) 的那个 Trie 节点。
        //curNode 总是代表着我们已经处理过的那部分字符串
        //初始：curNode代表的是空字符（root），sub(0,0)
        //保持：第一次循环后，代表的是第一个字符，sub(0,1)
        //结束：最后循环，代表的是最后的字符
                                    

    }

    public boolean startsWith(String prefix) {
        int cur = 0;
        TrieNode curNode = root;
        while (cur < prefix.length()){
            if (!curNode.map.containsKey(prefix.charAt(cur))){
                return false;
            }else {
                curNode = curNode.map.get(prefix.charAt(cur));
                cur++;
            }
        }
        return true;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

时空复杂度：

insert，时间O(l)

search，时间O(L)

startsWith，时间O(l)

空间：O(S)，其中 S 是所有插入单词的字符总数。在最坏情况下（所有单词没有公共前缀）

关于通配符回顾一下：

PECS。

PECS = Producer Extends, Consumer Super

Producer Extends (? extends T): 如果你的泛型结构是一个生产者（它只往外提供、产出数据），那么使用 extends。
Consumer Super (? super T): 如果你的泛型结构是一个消费者（它只往里获取、消费数据），那么使用 super。

1. `? extends V` (Producer Extends)

含义: “V 或者 V 的某个子类”。（extends常常表示继承，反正就是子类的意思，小于等于）
行为: 你可以把它想象成一个只读的容器。
你能做什么: 你可以安全地从这个结构中取出数据，因为无论取出的具体是哪个子类，它至少是一个 V 类型的对象。
你不能做什么: 你不能安全地向这个结构中存入数据（除了 null）。为什么？因为你不知道这个容器的确切类型。如果它是一个 List<? extends Fruit>，它可能是 List<Apple>，也可能是 List<Orange>。你不能把一个 Orange 存入一个 List<Apple> 中。编译器为了保证类型安全，干脆禁止了所有存入操作。

一句话总结 ? extends V: 我不知道具体是什么，但我知道它上限是 V。我只能从中读取 (Produce)，不能写入。

2. `? super K` (Consumer Super)

含义: “K 或者 K 的某个父类 (一直到 Object)”。（super常常表示调用父类，大于等于）
行为: 你可以把它想象成一个只写的容器。
你能做什么: 你可以安全地向这个结构中存入 K 类型的对象（以及 K 的子类对象）。为什么？因为无论这个容器的确切类型是 List<K>，还是 List<SomeParentOfK>，还是 List<Object>，它都能安全地容纳一个 K 类型的对象。
你不能做什么: 你不能安全地从中取出特定类型的数据（除了 Object）。为什么？因为你不知道里面存的到底是什么。如果它是一个 List<? super Apple>，它可能是 List<Fruit>，里面可能存着 Orange。你取出一个元素，只能保证它是一个 Object，但不能保证它是一个 Apple。

一句话总结 ? super K: 我不知道具体是什么，但我知道它下限是 K。我只能向其中写入 (Consume)，不能保证读取到特定类型。

200. 岛屿数量

994. 腐烂的橘子

207. 课程表

208. 实现 Trie (前缀树)

1. ? extends V (Producer Extends)

2. ? super K (Consumer Super)

1. `? extends V` (Producer Extends)

2. `? super K` (Consumer Super)